For early runs, set the convergence criteria loosely, or use Ctrl+F to stop the iterations.
If in doubt, set the convergence criteria very tightly for your final report, e.g.,
CONVERGE=B ; both LCONV= and RCONV= apply
LCONV= .0001 ; largest logit change .0001 logits
RCONV= .01 ; largest score residual .01 score points
MJMLE= 0 ; unlimited JMLE iterations
and be prepared to stop the iterations manually, if necessary, using "Finish Iterating", Ctrl+F, on the File pull-down menu
Remember that convergence criteria tighter than the reported standard error of a measure are somewhat of a numerical fiction.
The Rasch model is non-linear. This means that estimates cannot be obtained immediately and exactly, as can be done with the solution of simultaneous linear equations. Instead, estimates are obtained by means of a series of guesses at the correct answer.
The initial guess made by Winsteps is that all items are equally difficult and all persons equally able. The expected responses based on this guess are compared with the data. Some persons have performed better than expected, some worse. Some items are harder than expected, some easier. New guesses, i.e., estimates, are made of the person abilities and item difficulties, and also the rating (or partial credit) scale structures where relevant.
The data are again examined. This is an "iteration" through the data. Expectations are compared with observations, and revised estimates are computed.
This process continues until the change of the estimates is smaller than specified in LCONV=, or the biggest difference between the marginal "total" scores and the expected scores is smaller than specified in RCONV=. The precise stopping rule is controlled by CONVERGE=. When the estimates are good enough, the iterative process has "converged". Then iteration stops. Fit statistics are computed and the reporting process begins.
There are standard convergence criteria which are suitable for most small and medium-sized complete data sets. LCONV= is harder to satisfy for small complete data sets and many sparse data designs, RCONV= for large complete data sets.
The "least converged" persons (and items) are those that Winsteps is having the most difficulty estimating. This is not usually because their responses misfit the model but because their scores are extreme. It is more difficult to estimate the measure for a person who scores 1 out of 20 than of a person who scores 10 out of 20 (even if the 10 out of 20 greatly misfit the model). This is because Rasch estimation is done as though the data fit the model. Then, after the estimates have been made, the data are evaluated to determine the extent to which the data do fit the model. It is the same process in linear regression. The parameters are estimated as though the data fit the linear regression model. Then the data are investigated to see whether they do. It is at this later stage that outliers are detected. The Rasch model is a special case of logit-linear regression.
Anchored analyses
Anchor values always misalign somewhat with the current dataset unless they are estimated from it. Thus, the maximum residuals can never reduce to zero. Convergence occurs when the maximum logit change is too small to be meaningful. Accordingly, RCONV= is unproductive and only LCONV= is useful. Suggested specifications are:
CONVERGE = L ; only LCONV is operative
LCONV = .005 ; smaller than visible in standard, two decimal, output.
Missing data
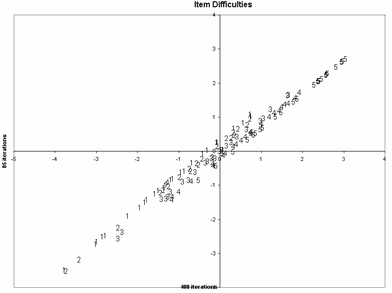
For some data designs much tighter criteria are required, particularly linked designs with large amounts of missing data. For instance, in a vertical equating design of 5 linked tests, standard convergence occurred after 85 iterations. Tightening the convergence criteria, i.e., using smaller values of LCONV= and RCONV=, convergence occurred after 400 iterations. Further iterations made no difference as the limit of mathematical precision in the computer for this data set had been reached. The plot shows a comparison of the item difficulties for the 5 linked tests estimated according to the standard and strict convergence criteria.
CONVERGE = B
LCONV = .001 ; 10 time stricter than usual
RCONV = .01 ; 10 times stricter than usual
Note that convergence may take many iterations, and may require manual intervention to occur: Ctrl+F.