By default, the structure or a rating scale (polytomy) is estimated from the data, and expressed as Rasch-Andrich thresholds. When the data are sparse, or the rating scale is long, there may not be enough observations to estimate every threshold securely. SFUNCTION= defines a smoothing function for estimating all the rating scale thresholds. If all the categories are not observed in the data, ISRANGE= defines the range of the category numbers.
Alternative approaches are described at Null or unobserved categories: structural and incidental zeroes, also at Unobserved and dropped categories.
Modeling Rasch-Andrich Thresholds for unobserved and sparse categories |
||
Example: Olympic Ice-Skating, Exam15.txt. The rating-scale is from 0.0 to 6.0, renumbered 00 to 60 for Rasch analysis. The empirical data are from the Pairs Figure-Skating at the Salt Lake City Olympics.
Category frequencies: Possible categories: 0-60 = 61 categories Observed categories: 29, 30-59 = 30 categories Unobserved categories: 00-28, 30, 60 = 31 categories |
||
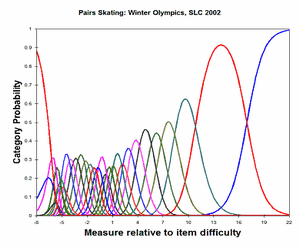
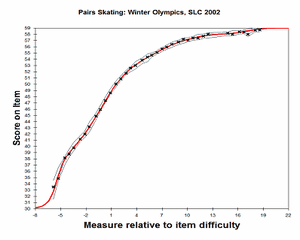
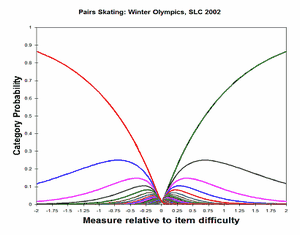
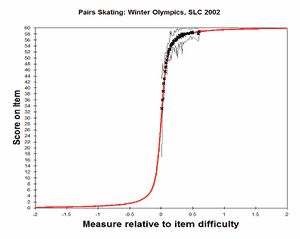
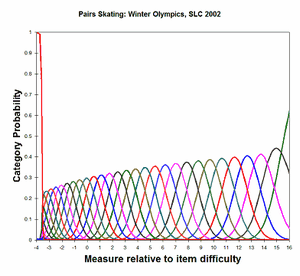
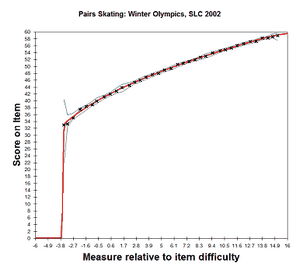
Analysis 1: Categories 29, 31-59 observed, renumbered 30-59. Estimated using the method of Wright, Masters (1982). CODES= " 29 31 32 33 34 35 36 37 38 39 40 41 42 43 44+ + 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59" NEWSCORE = " 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44+ + 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59" STKEEP=NO |
||
Category Probability Curves |
Item Characteristic Curves |
|
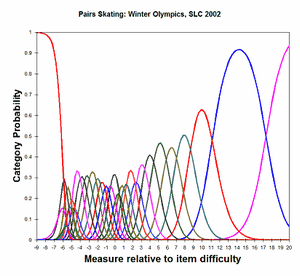
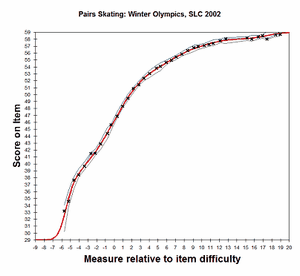
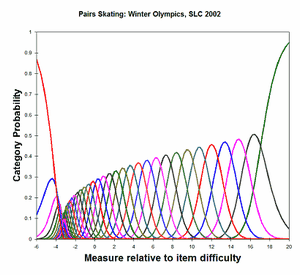
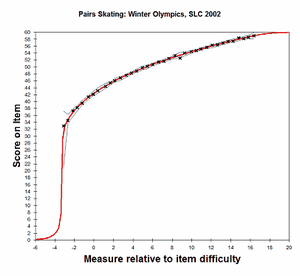
Analysis 2: Categories 29, 31-59 observed. Category 30 interpolated with Wilson (1991). CODES= " 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44+ + 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59" or CODERANGE= 29 - 59 STKEEP=YES |
||
|
|
|
Analysis 3: 1st moment (thresholds at central location). All thresholds have the same estimate. Categories 0-60. CODERANGE= 0 - 60 SFUNCTION=1 ; item thresholds are at item location. Threshold dispersion = 0. ISRANGE=* 1 0 60 ; 1 is item in the item-group: category range 0-60 * or |
||
|
|
|
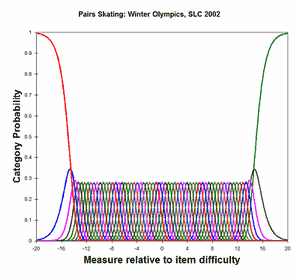
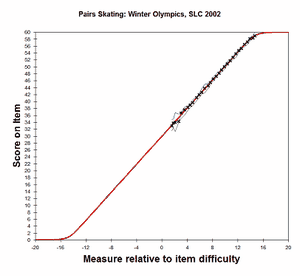
Analysis 4: 2nd moment (thresholds with uniform dispersion) . Thresholds have a linear relationship. Categories 0-60 with Andrich, Luo (2003), Pedler (1987) CODERANGE= 0 - 60 SFUNCTION=2 ISRANGE=* 1 0-60 * |
||
|
|
|
Analysis 5: 3rd moment (thresholds with dispersion and skewness). Thresholds have a quadratic relationship. Categories 0-60 with Andrich, Luo (2003), Pedler (1987) CODERANGE= 0 - 60 SFUNCTION=3 ISRANGE=* 1 0-60 * |
||
|
|
|
Analysis 6: 4th moment (thresholds with dispersion, skewness and kurtosis). Thresholds have a cubic relationship. Categories 0-60 with Andrich, Luo (2003), Pedler (1987) CODERANGE= 0 - 60 SFUNCTION=4 ISRANGE=* 1 0-60 * |
||
|
|
|
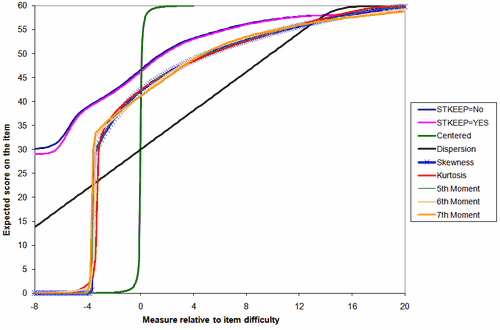
ICCs for these and higher moments
The 4th moment (kurtosis, red line, quartic) models the smoothest ICC for the full range of the rating scale 0-60. The higher moments (SFUNCTION=5,6,...) do not add meaningfully to the red line of the 4th moment (kurtosis, SFUNCTION=4). |
|
|
Andrich, D. & Luo, G. (2003). Conditional Pairwise Estimation in the Rasch Model for Ordered Response Categories using Principal Components. Journal of Applied Measurement, 4(3), 205-221. Pedler, P.J. (1987) Accounting for psychometric dependence with a class of latent trait models. Ph.D. dissertation. University of Western Australia. Wilson M. (1991) Unobserved or Null Categories. Rasch Measurement Transactions, 5:1, 158 - www.rasch.org/rmt/rmt51b.htm Wright B.D., Masters G.N. (1982) Rating Scale Analysis. MESA Press. |
||