"Structural Validity is defined as the degree to which the scores of the measurement instrument are an adequate reflection of the dimensionality of the construct being measured." De Vet HCW , Terwee CB, Mokkink LB, Knol DL. Measurement in Medicine. Cambridge, United Kingdom: Cambridge University Press; 2011.
Michael Commons asked: "What in Winsteps tells how unidimensional a fit is?"
The Rasch measures estimated by unidimensional Rasch models are forced to be unidimensional. Off-dimensional aspects of the data are in the part of the data not explained by the Rasch measures, i.e., the Rasch residuals. The Rasch residuals decompose into (a) the randomness predicted by the Rasch model, and (b) components on dimensions other than the unidimensional Rasch variable, (c) off-dimensional noise, such as random guessing.
In empirical data, (a) and (c) usually dominate (b), so that item-level or person-level fit statistics tend to be insensitive to multidimensionality, as R.P. McDonald (1985) reports. Accordingly we must focus on techniques that quantify (b), such as PCA of residuals. If the eigenvalues reported by PCA approximate the size predicted by the Rasch model, then the data are effectively unidimensional. Otherwise, the bigger the eigenvalues, the less unidimensional are the data.
Roderick P. McDonald, Factor Analysis and related methods. Hillsdale, NJ: Lawrence. Erlbaum Associates, 1985.
Multidimensionality is complicated, because it depends on the purpose of the instrument.
Here is a multidimensional instrument. It has 5 items: 1 geography item. 1 history item. 1 cooking item. 1 carpentry item. 1 arithmetic item.
This instrument is multidimensional, but none of its dimensions is big enough to make a unidimensional instrument. We cannot split this multidimensional instrument into unidimensional instruments, but that does not make the instrument unidimensional. However, we may decide that this instrument is measuring a general "education" variable, and declare that this instrument is unidimensional for our purposes.
For instance, an arithmetic test (addition, subtraction, multiplication, division) is unidimensional from the perspective of school administrators deciding whether a child should advance to the next grade-level, but the same test is multidimensional from the perspective of the school psychologist diagnosing learning difficulties. For instance, learning difficulties with subtraction in young children may indicate social maladjustment.
Also
Here is an example. We can proceed as follows:
a. Compare the Raw Variance explained by items (19.8%) with the Unexplained variance in 1st contrast (7.1%). Is this ratio big enough to be a concern? In your analysis, the Rasch dimension dominates (almost 3 times the secondary dimension), but the secondary dimension is noticeable.
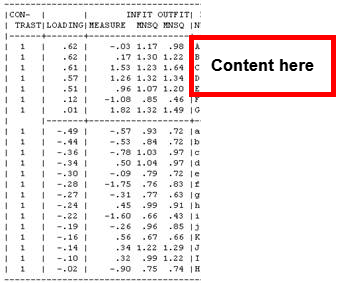
b. Is the secondary dimension bigger than chance? Eigenvalue = 2.8. This is the strength of 3 items. We do not expect a value of more than 2 items by chance. www.rasch.org/rmt/rmt191h.htm - and we would also need at least 2 items to think of the situation as a "dimension" and not merely an idiosyncratic item.
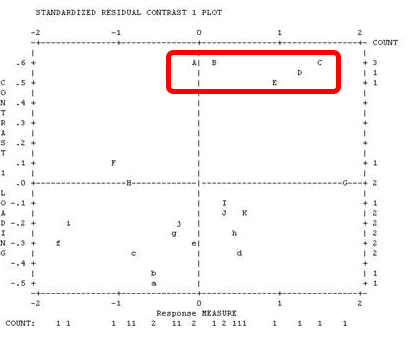
c. Does the secondary dimension have substance? Looking at your plot, we can see that items ABCDE are separated vertically (the important direction) from the other items. They are the core of the secondary dimension. 5 items are enough items that we could split them into a separate instrument (exactly as we could with "subtraction" on an arithmetic test).
Is this secondary dimension important enough, and different enough, that we would consider reporting two measures (one for ABCDE and one for the other items) rather than one measure for all items combined? The content of ABCDE appears to be psycho-social (e.g., one item includes the word "anxious" in this example). The other items are more physical (e.g., one item includes the word "walking" in this example). Consider the purpose of the instrument. Is "anxious" important or not? Is it part of the central purpose for the instrument? Would the instrument be improved or degraded (from a usefulness perspective) if items ABCDE were omitted? Would the instrument be improved or degraded (from a usefulness perspective) if a separate measure was reported for items like ABCDE?
d. Rasch-analyze the sample on the ABCDE items and then on the other items. Cross-plot the person measures.
Look at the correlation of the two sets of person measures (and the correlation disattenuated for measurement error). Is the correlation noticeably low? In this example, the disattenuated correlation was 0.82, indicating that the dimensions share explains about 67% of the person measure variance.
We expect most people to lie along a statistical diagonal. Who is off-diagonal? (Perhaps the people with social problems.) Are they important enough to merit a separate measurement system? For instance, on an English-language test, native-speakers of English, and second-language speakers usually have different profiles. Native speakers speak relatively better. Second-language speaker may spell relatively better. But two measures of English-language-proficiency are rarely reported.
If you decide that the secondary dimension is important enough to merit two measures, or the secondary dimension is off-dimension enough to merit omitting its items, then the instrument is multidimensional (in practice). If not, then the instrument is unidimensional (in practice), no matter what the statistics say.
Tentative guidelines based on the % of the sample are sampling dependent. If you are planning to apply a criterion such as "5% of the sample", then verify that your sample matches the intended target population of the instrument. In general, 5% seems very low. Would we institute a special measurement system for 1 child in a classroom of 20 children? Unlikely? We would probably need at least 4 children = 20% before we would consider reporting (and acting on) two measures.
In the USA, African-Americans comprise 13% of the population, and there is a debate about whether or not they should have special measurement systems. In some situations they do. And, similarly, whether there should be special provision for Spanish-speakers (15% of the USA population). In some situations there are. These percentages suggest that a threshold of about "10% of the sample" may be reasonable for separate measurement procedures.
My conclusion about this instrument (knowing nothing about its practical purpose) would be that the instrument is multidimensional and that items ABCDE should be omitted (or rewritten or replaced to emphasize their physical rather than their psychological aspects).
"Unidimensionality" is a choice based on the circumstances, so, if you are writing a paper, then please include a discussion of why (or why not) you decided that the instrument is multidimensional. This would be helpful to other researchers.
Table of STANDARDIZED RESIDUAL variance (in Eigenvalue units)
-- Observed -- Expected
Total raw variance in observations = 39.8 100.0% 100.0%
Raw variance explained by measures = 18.8 47.2% 48.0%
Raw variance explained by persons = 10.9 27.4% 27.8%
Raw Variance explained by items = 7.9 19.8% 20.1%
Raw unexplained variance (total) = 21.0 52.8% 100.0% 52.0%
Unexplned variance in 1st contrast = 2.8 7.1% 13.5%
Unexplned variance in 2nd contrast = 2.6 6.5% 12.3%
Unexplned variance in 3rd contrast = 2.1 5.4% 10.2%
Unexplned variance in 4th contrast = 1.7 4.4% 8.3%
Unexplned variance in 5th contrast = 1.6 4.0% 7.6%
1st contrast:
Question: My instrument has 200 items and my First Contrast has an eigenvalue of 9.2. Could this be explained by the large number of items analyzed?
Answer: Yes, the more items there are, then the more likely that a random cluster of items are inter-correlated by accident.
So, the first step with the potentially 9 or so items in a secondary dimension is to look at the plot in Winsteps Table 23.1. Is there a cluster of items at the top or bottom of the plot that share a content area that differs noticeably from the other items?
If so, this could be a secondary dimension. So, the next thing is to look at the table of correlations in Table 23.0. This reports the correlations of the person measures on the different clusters of items identified in the first contrast. Is the disattenuated correlation between the person measures on the suspect cluster of items and the person measures on the other items low or negative?
If so, the suspect cluster of items is measuring something different. It is a different dimension. When items on this secondary dimension are included with the items on the dominant dimension, then responses to the secondary items look like random noise from the viewpoint of the dominant dimension.
If not, the suspect cluster of items is probably a secondary strand in the content area, similar to "word problems" on an arithmetic test. Performance profiles of the person across strands will not be even, but will also not be contradictory.
The "variance explained" can be somewhat misleading because it is dominated by the variance of the item difficulties and the variance of the person abilities. We may be contrasting a wide range of abilities and/or difficulties on the dominant dimension against a narrow range of abilities and/or difficulties on the secondary dimension.
