T7LGS= and Juxtapose= control this Table. One table is produced for each arrangement of each facet which lists its elements and their estimates. The arrangement is determined by the Arrange= specification, otherwise it is ascending sequence by element number.
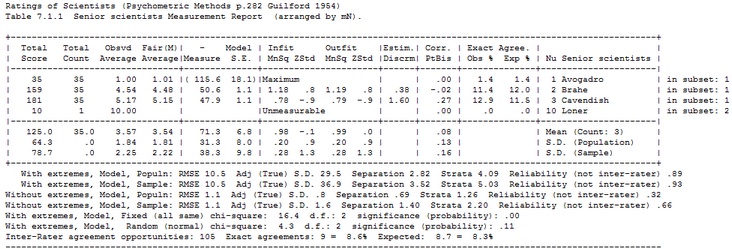
when there are Groups, each Group has its own Table. such as Table 7.1.1.1. Controlled by T7LGS=
Column Heading |
Meaning (values that are not estimable are blank) |
Total Score = (when Totalscore=Yes) |
the observed raw score (including extreme elements) |
Obsvd Score = Observed Score: (when Totalscore=No) |
observed raw score, the sum of the active responses for that element, after removal of extreme elements and renumbering of rating scales or partial credit scales to eliminate unobserved intermediate categories, when Keep= is not specified, so that Ordinal is active. |
Weightd Score = (when weighting is active) |
weighted: the observed raw score (including extreme elements) multiplied by their weights |
Total Count = (when Totalscore=Yes) |
the observed response count (including extreme elements). This is the sum of the weighted when the data are weighted. |
Obsvd Count = Observed Count: (when Totalscore=No) |
the number of active responses observed for the element |
Weightd Count = (when weighting is active) |
weighted: the observed response count (including extreme elements) multiplied by their weights |
Fair(M) Average = Fair Mean-based Average
|
Rasch measure to raw score conversion, producing an average rating for the element that is standardized so that it is fair to all elements in the facet, using the mean measures of the elements in each facet as the baseline. |
Fair(Z) Average = Fair Zero-based Average |
Rasch measure to raw score conversion, producing an average rating for the element that is standardized so that it is fair to all elements in the facet, using the facet local origins (zero points) as the baseline. |
(Anchoring status Character =) A, G, X or none |
none shown: the element is not anchored A - the element measure is anchored (preset, fixed) in Labels= G - the element measure is part of a group-anchor which includes extreme measures (if any). X - the element measure is part of a group-anchor which excludes extreme measures (if any). |
+- Measure |
Rasch measure/calibration of ability/difficulty/leniency etc. in log-odds units (logits) or user-scaled units based on Umean= and Uscale= (....) indicates that the measure is for an extreme score, estimated according to Xtreme=. + says this facet is positively oriented: higher score <-> higher measure - says this facet is negatively oriented: higher score <-> lower measure |
Model S.E. |
the smallest-possible standard error assuming all randomness in the data accords with the Rasch model (best case) |
Real S.E. |
the larger standard error assuming excess randomness in the data contradicts the Rasch model (worst case) |
(Element measurement status) |
"Anchored" = this element is anchored, but does not participate in this analysis. Shown when Omit-unobserved=No. "Minimum" = this element has the minimum possible extreme score. Fit statistics cannot be computed. "Maximum" = this element has the maximum possible extreme score. Fit statistics cannot be computed. "Unmeasurable" = this measure for this element cannot be estimated because its observations do not connect it with estimable elements "One datum" = this element has only one observation "Unknown" = this element is inestimable for unknown reasons. Please report this to www.winsteps.com |
Infit MnSq = Infit Mean-Square |
the information-weighted, inlier-pattern-sensitive, mean-square fit statistic, with expectation 1, and range 0 to infinity. Less than 1 indicates muting: too little variation, lack of independence. More than 1 indicates noise: unmodeled excess variation. A mean-square is a chi-squared fit statistic divided by its degrees of freedom. For the chi-squared value, d.f., and probability, see Scorefile= |
Infit Zstd = Infit Z-standardized t-statistic |
the Infit MnSq statistic standardized toward a unit-normal distribution so effectively a t-statistic with infinite degrees of freedom, i.e., a z-score. The accuracy of this standardization is data dependent. This tests the statistical hypothesis: "Does the Infit Mean-Square indicate that apparent randomness in these data fit the Rasch model exactly?" |
Outfit MnSq = Outfit Mean-Square |
the unweighted, outlier-sensitive, mean-square fit statistic, with expectation 1, and range 0 to infinity. Less than 1 indicates muting: too little variation, lack of independence. More than 1 indicates noise: unmodeled excess variation. A mean-square is a chi-squared fit statistic divided by its degrees of freedom. For the chi-squared value, d.f., and probability, see Scorefile= |
Outfit Zstd = Outfit Z-standardized t-statistic |
the Outfit MnSq statistic standardized toward a unit-normal distribution so effectively a t-statistic with infinite degrees of freedom, i.e., a z-score. The accuracy of this standardization is data dependent. This tests the statistical hypothesis: "Does Outfit Mean-Square indicate that the apparent randomness in these data fit the Rasch model exactly?" |
Estim. Discrm = Estimated Discrimination |
an estimate of the item discrimination computed according to the "two-parameter logistic model" (2-PL) and "Generalized Partial Credit Model" approach www.rasch.org/rmt/rmt181b.htm, but without allowing the discrimination estimate to alter other estimates. 1.0 is the expected value. Values higher than 1.0 indicate a steeper than expected empirical ICC. Values less than 1.0 indicate a flatter empirical ICC. Negative values indicate reverse discrimination. Inspect these on the Graphs menu. According to www.rasch.org/rmt/rmt142a.htm discriminations in the range 0.5 to 1.5 provide reasonable fit to the Rasch model. |
|
when a column with this heading is produced, it contains rough estimates of the displacements of the reported measures from those expected if: i) the analysis had reached convergence, or ii) the reported measure were not fixed at an anchored value. Displacements less than the convergence criteria or the measure standard errors are not reported here. They can be seen in the Scorefile=. When there are no displacements to report, this column is not produced. Displacement in logits = (observed raw score - expected raw score based on reported measure) / (model-derived raw-score variance) The reported Displacement is (Displacement in logits) * (uscale user-scaling) * (orientation of facet: positive or negative). This is limited to the range -10 to +10 logits. |
Correlation: PtMea = Point-measure correlation |
the correlation between the element's observations and the measures modeled to generate them. Produced by Pt-biserial=Measure |
Correlation: PtBis = Point-Biserial correlation (exclude) |
a many-facet version of the point-biserial correlation between observations and their corresponding average observations (excluding the current observation). Produced by Pt-biserial=Yes |
Correlation: PtBisI = Point-Biserial correlation (include) |
a many-facet version of the point-biserial correlation between observations and their corresponding average observations (including the current observation). Produced by Pt-biserial=Include |
Correlation: PtExp = Point-Correlation Expected value |
the expected value of the reported adjacent point-correlation. Use this for deciding whether a correlation is too high or too low. www.rasch.org/rmt/rmt221e.htm |
Exact Agreement: Obs % = Observed % |
percent of exact agreements between raters on ratings made under identical conditions, see Interrater= |
Exact Agreement: Exp % = Expected % |
expected percent of exact agreements between raters on ratings made under identical conditions based on their Rasch measures. Compare the Observed % with this value. |
Group |
the group number to which the element is assigned in Labels=. This is used for group-anchoring and group reporting. |
Weight |
weighting applied to observations of this element (defaults to 1.00) in Labels=. This multiples the weight (if any) specified in Models=, and the R weight specified with the observations (if any) and the Labels= weights of the other elements in the Data= specification for each active observation. |
N = number |
the element number in Labels= |
(Name of Facet in Labels=) |
element label in Labels= |
in subset: (numbers) |
the disjoint subsets of which this element is a member |
|
|
Mean (Count: ...) |
Average of its column for active elements with count of relevant elements |
S.D. (Population) |
the (smaller) standard deviation of all values in its column (relevant to this analysis), computed on the basis that the elements are the entire population of elements |
S.D. (Sample) |
the (larger) standard deviation of all values in its column (relevant to this analysis), computed on the basis that the elements are a random sample from a population of elements |
Reliabilities and Chi-squares |
|
Inter-rater Agreement |
The statistics in Table 7 are also in the Scorefile=, but it can be convenient to copy-and-paste line from Table 7 into Excel. These paste into one Excel column. The Excel "Data", "Text-to-Columns" splits the Table 7 lines into Excel columns.
