The computer program "Facets" implements the "many-facet Rasch measurement model" (Linacre, 1989). Each ordinal observation is conceptualized to be the outcome of an interaction between elements, e.g., a student, an item and a rater. These interacting elements are modeled to be operating independently and their measures to combine additively on the latent variable. For instance each rater is modeled to exhibit a specific amount of leniency or severity, and to act as an independent expert, not as a "scoring machine". The relationship between the ordinal observations and the linear measures of the elements is non-linear.
Danish Mathematician Georg Rasch (1960) constructed the necessary and sufficient mathematical model for the transformation of ordinal observations into linear measures. This model has the form of a logistic regression model, but each person and item is individually parameterized. In fact, it looks like a regression in which each item and each person is parameterized as a coefficient applied to a dummy variable. The dummy variable is "1" if the person or item participates in the observation, "0" otherwise. In principle this could be estimated with standard statistical software, but such software rarely allows for the estimation of the hundreds or thousands of parameters that can be encountered in just one Rasch analysis.
There are currently (2020) about 1,000 serious uses of the Facets software package. Many of these are in the medical field. This is probably because raters in that field behave like independent experts, the judging designs are irregular and pass-fail decisions for individuals (either for credentialing or patient treatment) are crucial. In contrast, in most educational testing situations, e.g., essay grading, raters are intended to behave like scoring machines, and the judging designs are regimented. Individual educational decisions are not of interest to educational administrators (unless theirs are the relevant children!) Thus, provided the random behavior is small (verified using G-theory), administrators are not interested in Facets-style corrections to student ability estimates.
The standard Rasch model for dichotomous data with persons and items is:
log ( Pni/(1-Pni)) = Bn - Di
where Pni is the probability that person n will succeed on item i, where person n has ability Bn and item i has difficulty Di. It can be seen that the model is additive in the parameters (Bn) and (-Di). Thus it meets the first requirement for interval measurement. From the estimation standpoint, the maximum-likelihood of the parameter estimate for each parameter occurs when the expected raw score corresponding to the parameter estimate equals the observed raw score. This is Fisher's principle of statistical sufficiency. The model has other nice properties, such as conjoint ordering, stochastic Guttman transitivity, concatenation, and infinite divisibility. This model has been applied productively to educational tests for over 40 years.
Statisticians can find it difficult to adjust to Rasch methodology. They tend to believe that the data points tell the truth and that it is the task of statisticians to find models which explain them and to find the latent variables which underlie them. Rasch methodology takes an opposite position. It says that the latent variable is the truth, and when that latent variable is expressed in linear terms, it is the Rasch model that is necessary and sufficient to describe it. Consequently those data points which do not accord with the Rasch model are giving a distorted picture of the latent variable. They may be telling us very important things, e.g., "the students were disinterested", "the scoring key was wrong" - but those do not pertain to the central variable .
The Rasch model has been extended to rating scale and partial credit observations, while maintaining the same mathematical properties. This "rating scale" model has been used successfully for 40 years in the analysis of attitude surveys and other rated assessments. An extended version of this model (Andrich, 1978, Masters 1982) is the grouped-item rating scale model:
log ( Pnik/Pni(k-1)) = Bn - Dgi - Fgk
where Pnik is the probability of observing category k for person n encountering item i.
Pni(k-1) is the probability of observing category k-1
Fgk is the difficulty of being observed in category k relative to category k-1, for an item in group g.
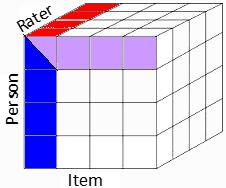
rows = person
columns = items
3rd dimension (slices) = raters
Among many other extensions to the Rasch model is the Many-Facets Rasch Model. This extends the polytomous form of the model:
log ( Pnijk/Pnij(k-1)) = Bn - Dgi - Cj - Fgk
Again, the mathematical properties of the model are maintained, but one (or more) extra components of the measurement situation are introduced. In this example, Cj, represents the severity (or leniency) of rater (judge) j, who awards the ratings {k} to person n on item i. As in the dichotomous model, the raw scores are the sufficient statistics for the Bn, Dgi and Cj. The counts of observations in each category are the sufficient statistics for estimating the {Fk}. The model also supports powerful quality-control fit statistics for assessing the conformance of the data to the model. The model is robust against many forms of misfit, so that the typical perturbations in data tend to have little influence on the measure estimates. A further feature of the model is its robustness against missing data. Since the model is parameterized at the individual observation level, estimates are obtained only from the data that has been observed. There is no requirement to impute missing data, or to assume the overall form of the distribution of parameters.
In estimating the measures, the model acts as though the randomness in the data is well-behaved. This is not a blind assumption, however, because the quality-control fit statistics immediately report where, and to what extent, this requirement has not been exactly met.
After measures have been constructed from data, they exist in a strictly linear frame of reference. This means that plots of the measures do, in fact, have the geometric properties generally assumed by unsophisticated readers to exist in all numbers. Ordinal numbers, such as the original ordered observations, do not have these strict geometric properties.
From the estimation perspective under JMLE, anchored and unanchored items appear exactly alike. The only difference is that anchored values are not changed at the end of each estimation iteration, but unanchored estimates are. JMLE converges when "observed raw score = expected raw score based on the estimates" for all unanchored elements and rating-scale categories. For anchored values, this convergence criterion is never met, but the fit statistics etc. are computed and reported by Facets as though it has been met. Convergence is based on the unanchored estimates. For more about estimation including CMLE, MMLE PMLE, see Estimation Considerations.
Historical Note on Inter-Rater Reliability:
Inter-rater Reliability is really slippery. Reliable in what way?
If we need raters to agree about who is better and who is worse, then correlations can work fine.
If we need raters to agree with the official ratings, often the aim of rater training, then a root-mean-square of the difference between the rater's ratings and the official ratings can work fine.
If we need raters to agree with who passes and who fails, then direct comparison of the ratings with the cut-point ratings can work fine up to a point. The problem here is rater leniency/severity. This goes all the way back to 1890 and the first mathematical study of rating. F. Y. Edgeworth, in his paper "The Element of Chance in Competitive Examinations", discovered that the spread of rater leniencies was about half the spread of person abilities. This has been seen many times since. In 1931, the "Conference on Examinations" (Eastbourne, England) tried to solve this problem mathematically, but they got bogged down in arguments between proponents of different standard statistical models. These models were descriptive, lacking any clear foundation in theory. It was not until 1986 that a solid foundation based on Rasch theory was constructed and solved the problem. This was the development of MFRM. a statistical methodology designed to produce linear measures that adjust for rater leniency and missing data with the minimum load on the raters, while also producing useful diagnostic information about each rater's behavior.
The benchmark paper for standard statistical approaches is Saal, F.E., Downey, R.G. and Lahey, M.A (1980) Rating the Ratings: Assessing the Psychometric Quality of Rating Data, Psychological Bulletin, 88(2), 413-428. There have been many methodological tweaks since then, but their message remains solid.
There were many papers written comparing MFRM with CTT and Generalizability Theory around 1990. In the Language Testing arena, https://www.winsteps.com/facetman/references.htm suggests 60 or so papers. (I have not kept this up to date, so there would be many more now.) The most comprehensive current comparison of standard statistics and MFRM is the book, "Introduction to Many-Facet Rasch Measurement" by Thomas Eckes published by Peter Lang. Probably also relevant, the book "Fairness, Justice and Language Assessment" by Tim McNamara, Ute Knoch, and Jason Fan published by Oxford UP.
