A standard error quantifies the precision of a measure or an estimate. It is the standard deviation of an imagined error distribution representing the possible distribution of observed values around their "true" theoretical value. This precision is based on information within the data. The quality-control fit statistics report on accuracy, i.e., how closely the measures or estimates correspond to a reference standard outside the data, in this case, the Rasch model.
S.E.s are produced by models of the data and are estimates of precision. For the S.E. of the mean, the model of the data is a normal distribution of the values summarized by the mean. The mean is an estimate, because we never know the true mean of a distribution. The S.E. shows the precision of the mean estimate. For the Rasch "model S.E.", the model is the Rasch model of ordinal data summarized by a parameter estimate. It is an estimate because we never know the true value of the parameter. The S.E. shows the precision of the Rasch estimate.
Standard errors of Rasch estimates reported by Winsteps do not include the imprecision in the estimates of all the other persons or items. When estimating the standard error for a person or item, the other persons and items are treated as though their distributions exactly match their populations and their estimated values are their true values. The imprecision in the estimates due to sampling errors and basing person estimates on item estimates, and vice-versa, is usually an order of magnitude less than the reported standard errors.
Note: Survey-style "sample" standard errors and confidence intervals are equivalent to Rasch item-calibration standard errors. So
Survey sample 95% confidence interval on a dichotomous (binary) item reported with a proportion-correct-value as a %
= 1.96 * 100% / (item logit standard error * sample size)
Example: survey report gives: p = 90%, sample size=100, confidence interval (95%) = 90±6%
Winsteps: logit S.E. of item calibration = 1/sqrt(100*.9*.1) = ±.33 logits.
So survey C.I. % = ±1.96 * 100 /(.33 * 100) = ±6%
Standard Errors of Items
The size of a standard error of an estimate is most strongly influenced by the number of observations used to make the estimate. We need measurement precision (standard error size) adequate for the purpose for which we are using the measures.
Probably the only time we need to be concerned about item standard errors within a test is when we want to say "Item A is definitely more difficult than Item B". For this to be true, their measures need to be more than 3 S.E.s different.
When comparing item difficulties estimated from different datasets, we use the item standard errors to identify when differences between the item difficulties of the same item are probably due to chance, and when they may be due to a substantive change, such as item drift.
Model "Ideal" Standard Error
The highest possible precision for any measure is that obtained when every other measure is known, and the data fit the Rasch model. The model standard error is 1/square root (Fisher information). For well-constructed tests with clean data (as confirmed by the fit statistics), the model standard error is usefully close to, but slightly smaller than, the actual standard error. The "model" standard error is the "best case" error. It is the asymptotic value for JMLE. For dichotomous data this is, summed over items i=1,L for person n, or over person n=1,N for item i:
![]()
For polytomies (rating scales, partial credit, etc.), with categories j=0,m:
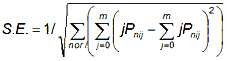
and, for the Rasch-Andrich thresholds,
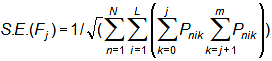
where Pnik is the probability of observing category k for person n on item i.
Misfit-Inflated "Real" Standard Error
Wright and Panchapakesan (1969) www.rasch.org/memo46.htm discovered an important result for tests in which each examinee takes more than a handful of items, and each item is taken by more than a handful of examinees: the imprecision introduced into the target measure by using estimated measures for the non-target items and examinees is negligibly small. Consequently, in almost all data sets except those based on very short tests, it is only misfit of the data to the model that increases the standard errors noticeably above their model "ideal" errors. Misfit to the model is quantified by fit statistics. But, according to the model, these fit statistics also have a stochastic component, i.e., some amount of misfit is expected in the data. Discovering "perfect" data immediately raises suspicions! Consequently, to consider that every departure of a fit statistic from its ideal value indicates failure of the data to fit the model is to take a pessimistic position. What it is useful, however, is to estimate "real" standard errors by enlarging the model "ideal" standard errors by the model misfit encountered in the data.
Recent work by Jack Stenner shows that the most useful misfit inflation formula is
Real S.E. of an estimated measure = Model S.E. * Maximum [1.0, sqrt(INFIT mean-square)]
In practice, this "Real" S.E. sets an upper bound on measure imprecision. It is the "worst case" error. The actual S.E. lies between the "model" and "real" values. But since we generally try to minimize or eliminate the most aberrant features of a measurement system, we will probably begin by focusing attention on the "Real" S.E. as we establish that measurement system. Once we become convinced that the departures in the data from the model are primarily due to modeled stochasticity, then we may base our decision-making on the usually only slightly smaller "Model" S.E. values.
What about Infit mean-squares less than 1.0? These indicate overfit of the data to the Rasch model, but do not reduce the standard errors. Instead they flag data that is lacking in randomness, i.e., is too deterministic. Guttman data are like this. Their effect is to push the measures further apart. With perfect Guttman data, the mean-squares are zero, and the measures are infinitely far apart. It would seem that inflating the S.E.s would adjust for this measure expansion, but Jack Stenner's work indicates that this is not so. In practice, some items overfit and some underfit the model, so that the overall impact of low infit on the measurement system is diluted.
Standard Errors with Anchor Values
Anchored measures are shown in the Winsteps output Tables with "A". These are set with IAFILE=, PAFILE= and SAFILE=. Anchor values are exactly precise with zero standard error. But each anchor value is reported with a standard error. This is the standard error that the anchor value would have if it were the freely estimated maximum-likelihood value of the parameter.
Plausible Values
"Plausible values" are random draws from a parameter's posterior distribution. Here the posterior distribution is a normal distribution of N(mean=estimated measure, S.D.=standard error) for each parameter. Plausible values would be random draws from this distribution. The Excel formula to do this is =(Measure + S.E.*NORMSINV(RAND( ))) which can be input into an extra column in a PFILE= or IFILE= written to Excel.
