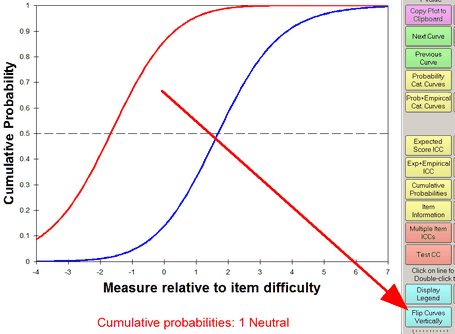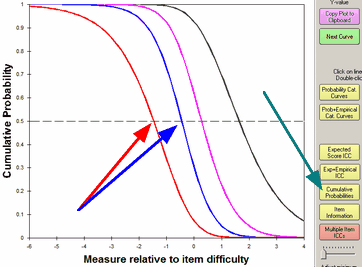
Select by clicking on "Cumulative Probabilities" or from the Graphs menu.
Lines: This shows the modeled category probability curves accumulated so that the left-hand curve (red) is the probability of being observed in the lowest category. The next curve (blue) is the probability of being observed in the lowest or next lowest category. And so on to the right. If the categories are number 1, 2, 3, 4, 5. Then the red line is the probability of observing category 1. The blue line is the probability of observing categories 1 or 2. The pink line is the probability of observing categories 1 or 2 or 3. The black line is the probability of observing categories 1 or 2 or 3 or 4. The probability of observing categories 1 or 2 or 3 or 4 or 5 (which includes every category) is 1.0 and corresponds to the upper side of the graph box.
The cumulative probability is the y-axis in this graph, but is the x-axis in G.N. Masters (1988) "The Analysis of Partial Credit Scoring" (Figure 2), Applied Measurement in Education, 1:4, 279-297. The cumulative probability accumulates the probabilities across the categories upwards from low category to high category (or vice versa) for any ability level.
Arrows: The points of intersection between these curves and the 0.5 probability line are the Rasch-Thurstonian thresholds. The points at which being observed in this category (or below) and the category above (or higher) are equal. These curves are always in the order of the category scores. The red arrow points to the Thurstonian threshold where the probability of observing category 1 and of observing categories 2 or 3 or 4 or 5 are equal. The is called the Thurstonian threshold for Category 2. The blue arrow points to the Thurstonian threshold where the probability of observing categories 1 or 2 and of observing categories 3 or 4 or 5 are equal. The is called the Thurstonian threshold for Category 3. The interval between the Thurstonian Threshold for Category 2 and the Thurstonian Threshold for Category 3 is one definition of the interval for category 2 on the latent variable.
Buttons are described in Graph window.
Click on the "Flip Curves Vertically" button to change the vertical direction of the curves. This reverses the definition of the cumulative probability curves. When flipped the red line in the plot above is the probability of observing categories 2 or 3 or 4 or 5. The flipped blue line in the plot above is the probability of observing categories 3 or 4 or 5. The flipped pink line is the probability of observing categories 4 or 5. The black line is the probability of observing category 5. Flipping the curves does not change the Thurstonian Thresholds. The red arrow continues to point to the Thurstonian Threshold for category 2.