In Rasch analysis, we use item correlations as an immediate check that the response-level scoring makes sense. If the observed correlation is negative, something may have gone wrong (MCQ miskey, reversed survey item, etc.)
In general, correlations are much too difficult to interpret, so we switch over to using mean-squares. The "expected correlation" indicates when conventional rules such as eliminate items with point-biserials less than 0.2 are misleading.
Item correlations are difficult to interpret because they are influenced by:
1. predictability of the data
2. targeting of the item on the person sample
3. distribution of the person sample
In Rasch analysis, we are chiefly concerned about the predictability of the data when assessing item quality, so we examine the predictability directly using the mean-square statistics, rather than indirectly through the correlations.
All correlations are computed as Pearson product-moment correlation coefficients. If you wish to compute other correlations, the required data are in XFILE= IPMATRIX=, IFILE= or PFILE=. The Biserial correlation can be computed from the point-biserial.
Point-Biserial and Point-Measure Correlations |
|||
Control Instruction |
Column Label |
Explanation |
Expected value (EXP.) |
PTBISERIAL= Yes PTBISERIAL= Exclude |
PBSX PTBISERL-EX
|
Point-biserial (or point-polyserial) correlation excluding the current observation from the raw score. Computes the point-biserial or point-polyserial correlation coefficients, rpbis, for persons and items. This is the Pearson product-moment correlation between the scored responses (dichotomies and polytomies) and the "rest scores", the corresponding total (marginal) scores excluding the scored responses to be correlated. This is a point-biserial correlation for dichotomies, or a point-polyserial correlation for polytomies. Extreme (perfect, maximum possible and zero, minimum possible) scores are included in the computation, but missing observations are omitted pairwise. The Biserial correlation can be computed from the Point-biserial. This correlation loses its meaning when there are missing data or with CUTLO= or CUTHI=. Specify PTBISERIAL=X instead.
In Table 14.1, etc., and IFILE= For each item, this correlates the current observation with the (raw score - current observation) The actual number of observations summed into the raw score is ignored.
In Table 14.3, etc., and DISFILE= For each item, each possible response option is evaluated in turn. •If the option matches the current observation and is not missing, then the option is score 1, if not the option is scored 0. Missing observations are ignored. Then the scored option is correlated with the (raw score - current observation) . •if the option matches the current observation and is missing, then the option is score 1, if not the option is scored 0 including different missing observation options. :Then the scored option is correlated with the raw score. |
PBSX-E PBX-E |
PTBISERIAL= All PTBISERIAL= Include |
PBSA PTBISERL-AL
|
Point-biserial correlation for all observations including the current observation in the raw score. Computes the Pearson correlation between the total (marginal) scores including all responses and the responses to the targeted item and person. This is a point-biserial correlation for dichotomies, or a point-polyserial correlation for polytomies. This correlation loses its meaning when there are missing data or with CUTLO= or CUTHI=. Specify PTBISERIAL=N instead. |
PBSA-E PBA-E |
PTBISERIAL= No PTBISERIAL= RPM PTBISERIAL= Measure PTMEASURE=Measure |
PTMA PTMEASUR-AL
|
Point-measure correlation for all observations. Computes the Pearson point-measure correlation coefficients, rpm between the observations and the measures, estimated from the raw scores including the current observation or the anchored values. Measures corresponding to extreme scores are included in the computation. |
PTMA-E PMA-E |
PTBISERIAL= X PTMEASURE=X |
PTMX PTMEASUR-EX |
Point-measure correlation excluding the current observation from the estimation of the measure. Computes the Pearson point-measure correlation coefficients, rpm between the observations and the measures or anchor values adjusted to exclude the current observation. Measures corresponding to extreme scores are included in the computation. This is an approximation to the exact value. See "Numerical Example" |
PTMX-E PMX-E |
PTBISERIAL= Skip |
---- |
Point- correlations are not computed. This speeds up estimation process. |
---- |
Point-correlations are always reported for items. Point-correlations are reported for persons when (i) all the items are dichotomies, (ii) all the items have three categories, or (iii) all the items are in the same item group (Andrich Rating Scale Model). Otherwise, the observed and expected correlations are reported as zero in PFILE=.
Example: Here are the point-biserial-type coefficient options for Example0.txt, Item 1 (Watch Birds).
Control Instruction |
PTBISERIAL= ALL |
PTBISERIAL= YES |
PTBISERIAL= NO |
PTBISERIAL= X |
Calculation: Correlate observation with |
raw score |
raw score - current observation |
Rasch measure |
Rasch measure estimated from |
Table 14, etc., Heading |
PTBISERL-AL |
PTBISERL-EX |
PTMEASURE-A |
PTMEASUR-EX |
PBSA |
PBSX |
PTMA |
PTMX |
|
Observed correlation |
.69 |
.66 |
.64 |
.61 |
Expected correlation (-E) |
.53 |
.47 |
.49 |
.48 |
In Table 14.1 and other measure Tables: Point-Biserial Correlations for dichotomies, and Point-Polyserial for polytomies
when PTBISERIAL=Yes
PTBSE is the point-biserial correlation between the responses to this item by each person and the total marginal score by each person (omitting the response to this item). This is the "point-biserial corrected for spuriousness". Henrysson, S. (1963). Correction for item-total correlations in item analysis. Psychometrika, 28, 211-218.
when PTBISERIAL=All
PTBSA is the point-biserial correlation between the responses to this item by each person and the total marginal score by each person (including the response to this item). This is the conventional point-biserial.
In Table 14.3 and other or distractor Tables:
when PTBISERIAL=Yes or PTBISERIAL=All
PTBSD is the distractor point-biserial correlation between the indicated response to this item (scored 1 and other responses scored 0) by each person and the total marginal score by each person.
There is a closer match between Table 14.1 and Table 14.3 when PTBISERIAL=All
PTBIS=Y or E (indicated by PTBSE): The point-biserial correlation rpbis for item i (when i=1,L for persons n=1,N) is the correlation between the observation for each person on item i and the total score for each person on all the items excluding item i (and similarly for the point-biserial for each person):
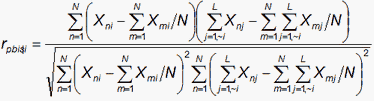
PTBIS=All (indicated by PTBSA): All the observations are included in the total score:
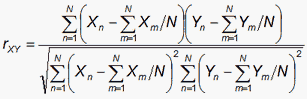
where X1,..,XN are the responses, and Y1,..,YN are the total scores. The range of the correlation is -1 to +1.
Under classical (raw-score) test theory conventions, point-biserial correlations should be 0.3, 0.4 or better. Under Rasch conditions, point-biserial (or point-measure) correlations should be positive, so that the item-level scoring accords with the latent variable, but the size of a positive correlation is of less importance than the fit of the responses to the Rasch model, indicated by the mean-square fit statistics.
Point-Measure Correlations
PTBIS=No (indicated by PTMEA): The correlation between the observations and the Rasch measures:
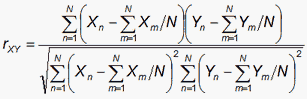
where X1,..,XN are the responses by the persons (or on the items), and Y1,..,YN are the person measures (or the item easinesses = - item difficulties). The range of the correlation is -1 to +1.
Jaspen, N. (1946) "Serial Correlation", Psychometrika, 11, 23-30.
Olsson, U., Drasgow, F. and Dorans, N.J. (1982) "The Polyserial Correlation Coefficient", Psychometrika, 47, 337-347.
The Expected Value of a Correlation
Interpreting an observed value is made easier if we can compare it with its expected value. Is is much higher than expected or much lower than expected?
The general formula for a Pearson correlation coefficient is shown above. Suppose that Xn is Xni the observation of person n on item i. Yn is Bn the ability of person n, then the point-measure correlation is:
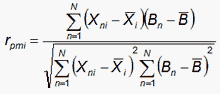
According to the Rasch model, the expected value of Xni is Eni and its model variance around the expectation is Wni. For dichotomies, Eni is the Rasch probability of success and Wni = Eni(1-Eni). For polytomies, Eni and Wni are given by RSA, p. 100 also at www.rasch.org/rmt/rmt34e.htm. For JMLE estimates, Sum(Eni) = Sum(Xni) for n=1,N. Thus an estimate of the expected value of the point-measure correlation is given by the Rasch model proposition that: Xni = Eni ±√Wni. Other variance terms are much smaller.
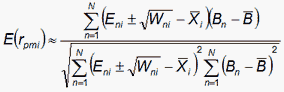
±√Wni is a random residual with mean 0 and variance Wni. Its cross-product with any other variable is modeled to be zero. Thus, simplifying,
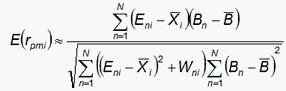
and similarly for the point-biserial correlations. Here is an example point-measure correlation and its expected value computed with an Excel spreadsheet:
Xni |
Xni-Xi |
(Xni-Xi)2 |
Bn |
Bn-B |
(Bn-B)2 |
(Xni-Xi)(Bn-B) |
Eni |
Eni-Xi |
(Eni-Xi)(Bn-B) |
Eni(1-Eni) = Wni |
(Eni-Xi)2 + Wni |
0 |
-0.50 |
0.25 |
-1.33 |
-1.66 |
2.74 |
0.83 |
0.16 |
-0.34 |
0.56 |
0.13 |
0.25 |
1 |
0.50 |
0.25 |
-0.03 |
-0.36 |
0.13 |
-0.18 |
0.41 |
-0.09 |
0.03 |
0.24 |
0.25 |
0 |
-0.50 |
0.25 |
1.33 |
1.01 |
1.01 |
-0.50 |
0.73 |
0.23 |
0.23 |
0.20 |
0.25 |
1 |
0.50 |
0.25 |
1.33 |
1.01 |
1.01 |
0.50 |
0.73 |
0.23 |
0.23 |
0.20 |
0.25 |
average Xi = 0.50 |
|
(i) ∑ = 1.00 |
average B = 0.33 |
|
(ii) ∑ = 4.89 |
(iii) ∑ = 0.65 |
|
|
(iv) ∑ = 1.05 |
|
(v) ∑ = 1.00 |
Observed point-measure Correlation = (iii) / √ ((i)(iii)) = |
0.29 |
||||||||||
Expected point-measure Correlation = (iv) / √ ((v)(ii)) = |
0.47 |
||||||||||
Difficulty of item i = 0.35 logits |
|||||||||||
Table courtesy of Peter Karaffa
Point-Correlations and the Partial Credit Model or Grouped Rating Scale Model: ISGROUPS=
The usual computations for correlation coefficients assume that all scores or measures within each of the two variables is in the same metric. For instance, when correlating age with height for children, the ages are all in months and the heights are all in centimeters. If we mix ages in months with ages in years, or height in centimeters with height in inches, then the age-height correlations can become meaningless.
The same situation can arise when we use the Partial Credit Model (ISGROUPS=0) or Grouped Rating Scale Model (ISGROUPS=AABB..). In particular, the Expected value of a Point-Correlation can be reported as negative. This is a warning is that the reported correlations are meaningless.
Disattenuated correlation coefficients
"Attenuated" means "reduced". "Disattenuation" means "remove the attenuation".
The observed correlation between two variables is attenuated (reduced toward zero) because the variables are measured with error. So, when we remove the measurement error (by a statistical operation), the resulting correlation is disattenuated. Disattenuated correlations are always further from zero.
Algebraically:
{A} and {B} are the "true" values of two variables. Their true (disattenuated) correlation is
Disattenuated ("true") correlation = r(A,B)
But the observed values of the variables are measured with error {A±a}, {B±b}, so the observed correlation is
observed correlation = r(A,B) * √(var(A)*var(B))/√((var( + a +a ²)*(var( + b + b ²)).
"Disattenuation" reverses this process.
If the reliability of {A} is RA, and the reliability of {B} is RB, then the disattenuated correlation between {A} and {B} is:
disattenuated r(A,B) = r(A,B) / √(RA*RB).
Point-Correlations in Table 14.1, Table 14.3, etc. and DISFILE= and IFILE=
For the item point-biserial correlations, PTBISERIAL=A and PTBISERIAL=E:, scored observations are correlated with their corresponding person raw scores.For the point-measure correlations, PTBISERIAL=M, scored observations are correlated with their corresponding Rasch measures.
Each response code (scored or "missing") is correlated only with scored response codes. With PTBISERIAL=Yes or All, the correlation is between the occurrence and the person raw score, indicated by PTBSD CORR. When this correlation is high positive for a correct MCQ option, then the item exhibits convergent validity. When this correlation is low or negative for incorrect MCQ options, then the item exhibits discriminant validity. Krus, D. J. & Ney, R. G. (1978) Convergent and discriminant validity in item analysis. Educational and Psychological Measurement, 38, 135-137.
Each scored response code is correlated only with the other scored codes: "1" for target code "0" for other scored codes. . Missing responses are correlated with all responses.
PTBSA CORR is PTBIS = All (include the current item in the person score)
PTBSE CORR is PTBIS = Yes (exclude the current item in the person score)
PTMEA CORR is PTBIS = No (correlate with the person measure)
The "Missing" point-measure correlation is the correlation between the raw scores for the persons and the responses to the item with "missing" scored 1 and the other responses scored 0.
The category (or option) correlation is always computed the same way:
1. We focus on a particular response to a particular item.
2. Everyone who chose that response to the item is scored "1", everyone else is scored "0". Missing data are ignored.
3. The scores of "1" or "0" are correlated with the person measures.
4. We do this for every response to every item.
For the distractor/option correlations reported in Table 14.3 and DISFILE=
For each item and each option, a correlation is computed for each code in CODES= in turn:
If the response in the data file is the current code, then a value of 1 is assigned
If the response in the data file is not the current code but is scored, then a value of 0 is assigned
If the response in the data file is not in CODES= and is scored with MISSING-SCORED=, then a value of 0 is assigned.
If the response in the data file is not in CODES= and is not scored with MISSING-SCORED=, then the response is ignored.
For each value of 0 or 1, the corresponding average response score is computed = (raw score / count scored observations)
The correlation is between the (weighted) values and the average response scores or Rasch measures
For each item, one correlation is computed for all codes in the data not in CODES=
If the response in the data file is not in CODES=, then a value of 1 is assigned
If the response in the data file is in CODES=, then a value of 0 is assigned
For each value of 0 or 1, an average response score is computed = (raw score / count scored observations)
The correlation is between the weighted values and the average response scores or Rasch measures
Point-Correlations with Missing Data
The Point-Biserial is not defined for incomplete data, so Winsteps applies the following formula::
•Missing observations are ignored when calculating the correlation
•Point-measures: Measures are already adjusted for missing data, so they are correlated directly with the scored observations
•Point-biserials: Raw scores are divided by their counts of scored responses, giving an average observation. These averages are correlated with the scored observations.
Suggestion: since the point-biserial is not defined when there is unscored missing data, please use the point-measure correlation, PTBISERIAL=M.
Example 1: Point-Measure Correlations (PTBIS=No) of Person Measures with Item 6 Options a,b,c,d, with b scored 1, and missing data, x.
Person measure |
Score on item 6 |
Person's response to item 6 |
Option a |
b |
c |
d |
x missing data |
0.5 |
0 |
d |
0 |
0 |
0 |
1 |
0 |
0.8 |
0 |
c |
0 |
0 |
1 |
0 |
0 |
0.9 |
1 |
b |
0 |
1 |
0 |
0 |
0 |
0.4 |
0 |
d |
0 |
0 |
0 |
1 |
0 |
1.0 |
0 |
a |
1 |
0 |
0 |
0 |
0 |
1.2 |
1 |
b |
0 |
1 |
0 |
0 |
0 |
2.0 |
- |
x |
- |
- |
- |
- |
1 |
Table 14.1 IFILE= |
PTBIS= NO 0.64 |
Table 14.3 DISFILE= |
PTBIS= NO 0.32 |
0.64 |
0.00 |
-0.89 |
0.85 |
Item difficulty: |
1.50 |
Mean ability: |
1.00 |
1.05 |
0.80 |
0.45 |
2.00 |
Example 2: Point-Biserial (Polyserial) Correlations (PTBIS=Yes) of Person Raw Scores (excluding current item) with Item 6 Options a,b,c,d, with b scored 1, and missing data, x.
Person score on all 20 items |
Missing (unscored) responses |
Average scored response |
Score on item 6 |
Person score excluding item 6 |
Average scored response excluding item 6 |
Person's response to item 6 |
Option a |
b |
c |
d |
x missing data |
10 |
0 |
10/20 |
0 |
10 |
10/19 |
d |
0 |
0 |
0 |
1 |
0 |
11 |
0 |
11/20 |
0 |
11 |
11/19 |
c |
0 |
0 |
1 |
0 |
0 |
12 |
0 |
12/20 |
1 |
11 |
11/19 |
b |
0 |
1 |
0 |
0 |
0 |
13 |
0 |
13/20 |
0 |
13 |
13/19 |
d |
0 |
0 |
0 |
1 |
0 |
14 |
0 |
14/20 |
0 |
14 |
14/19 |
a |
1 |
0 |
0 |
0 |
0 |
15 |
1 |
15/19 |
1 |
14 |
14/18 |
b |
0 |
1 |
0 |
0 |
0 |
16 |
2 |
16/18 |
- |
16 |
16/18 |
x |
- |
- |
- |
- |
1 |
Table 14.1 IFILE= |
|
PTBIS= ALL 0.47 |
|
|
PTBIS= YES 0.24 |
Table 14.3 DISFILE= |
PTBIS= YES 0.43 |
0.24 |
-0.33 |
-0.32 |
0.71 |
Statistical Significance of a Correlation
Null hypothesis is that the correlation is 0.00.
Student's significance test: t = r / sqrt[ (1—r2) / (N—2) ] with N-2 d.f. where N is the count of correlated cases.
Null hypothesis is that the correlation is another value, not 1 or -1
1. Use Fisher z' transformation to linearize hypothesized correlation and observed correlation:
z' = .5[ln(1+r) - ln(1-r)]
2. normal z = ( z'(observed) - z'(hypothesized) ) * sqrt (N-3)
Null hypothesis is that the correlation is 1 or -1
Use a number that means the same thing: 0.99 or -0.99
