For a score-to-measure table for fewer items, use ISELECT= or IDELETE= from the Specification Menu dialog box.
Table 20.2 Person score and measure distribution
Table 20.3 Complete score-to-calibration table for tests based on whole sample
TABLE OF MEASURES ON TEST OF 13 ITEM
----------------------------------------------------------------------------
| SCORE MEASURE S.E. | SCORE MEASURE S.E. | SCORE MEASURE S.E. |
|------------------------+------------------------+------------------------|
| 13 -6.34E 1.82 | 40 -1.35 .28 | 67 1.33 .35 |
| 14 -5.15 .99 | 41 -1.27 .28 | 68 1.46 .36 |
....
| 36 -1.65 .28 | 63 .84 .35 | 90 6.04 1.03 |
| 37 -1.58 .28 | 64 .96 .35 | 91 7.29E 1.84 |
| 38 -1.50 .28 | 65 1.08 .35 | |
| 39 -1.43 .28 | 66 1.21 .35 | |
----------------------------------------------------------------------------
CURRENT VALUES, UMEAN=.0000 USCALE=1.0000
TO SET MEASURE RANGE AS 0-100, UMEAN=46.5329 USCALE=7.3389
TO SET MEASURE RANGE TO MATCH RAW SCORE RANGE, UMEAN=49.2956 USCALE=5.7243
Predicting Score from Measure: Score = Measure * 8.2680 + 38.9511
Predicting Measure from Score: Measure = Score * .1158 + -4.5099
Maximum statistically different levels of performance (strata) = 3.8
Wright's Sample-independent Person (Test) Reliability based on maximum strata = .94
TOTALSCORE= YES includes extreme (maximum possible score and minimum possible score) for example file: Exam1.txt
TABLE OF MEASURES ON TEST OF 18 TAP (includes 4 extreme items)
----------------------------------------------------------------------------
| SCORE MEASURE S.E. | SCORE MEASURE S.E. | SCORE MEASURE S.E. |
|------------------------+------------------------+------------------------|
| 0 -8.86E 1.90 | 7 -2.97 .81 | 14 3.75 .94 |
| 1 -8.11E 1.90 | 8 -2.27 .87 | 15 4.64 .97 |
| 2 -7.37E 1.89 | 9 -1.41 .99 | 16 5.72 1.16 |
| 3 -6.62E 1.88 | 10 -.28 1.11 | 17 7.14E 1.90 |
| 4 -5.26 1.11 | 11 .93 1.06 | 18 7.87E 1.92 |
| 5 -4.32 .88 | 12 1.95 .98 | |
| 6 -3.62 .81 | 13 2.87 .95 | |
----------------------------------------------------------------------------
TOTALSCORE= NO excludes extreme (maximum possible score and minimum possible score) for example file: Exam1.txt
TABLE OF MEASURES ON TEST OF 14 NON-EXTREME TAP
----------------------------------------------------------------------------
| SCORE MEASURE S.E. | SCORE MEASURE S.E. | SCORE MEASURE S.E. |
|------------------------+------------------------+------------------------|
| 0 -6.62E 1.88 | 5 -2.27 .87 | 10 2.87 .95 |
| 1 -5.26 1.11 | 6 -1.41 .99 | 11 3.75 .94 |
| 2 -4.32 .88 | 7 -.28 1.11 | 12 4.64 .97 |
| 3 -3.62 .81 | 8 .93 1.06 | 13 5.72 1.16 |
| 4 -2.97 .81 | 9 1.95 .98 | 14 7.14E 1.90 |
----------------------------------------------------------------------------
In Table 20.1 |
Explanation |
TABLE OF MEASURES ON TEST OF 13 ITEM
TOTALSCORE=Yes includes extreme items TOTALSCORE=No excludes extreme items (if any) |
Raw score-to-Measure Table for all raw scores on the complete set of all active non-extreme calibrated items. This can also be output with SCOREFILE=.
Table 20.1 shows the score-to-measure table for persons with complete data. For persons with missing data, this table does not apply.
Score-to-measure tables for subtests or persons with missing data can be produced by using ISELECT= or IDELETE= from the Specification menu before requesting Table 20.
If there are subsets, then the reported Table 20 is one of an infinite number of possible Table 20s. |
SCORE |
Raw score on the complete set of non-extreme or all items. If IWEIGHT= produces decimal scores, then scores with one decimal place are shown. Some SCOREs may not be observable. Some observable scores may not be shown, but may be better approximated from TCCFILE= |
MEASURE |
Estimated measure for the SCORE raw score on all the items, adjusted by USCALE= and UIMEAN=, if active. The MEASURE may differ slightly from Table 17. Tighten convergence to make them agree exactly.
The SCOREFILE= and Table 20 person ability estimates are estimated on the basis that the current item difficulty estimates are the "true" estimates. These are the person estimates if you anchored (fixed) the items at their reported estimates. The convergence criterion used are LCONV= 0.01 and RCONV= 0.01 - these are considerably tighter than for the main analysis. So Table 20 is a more precise estimate of the person measures based on the final set of item difficulties.
PFILE=, Table 17 and the other Person Measure Tables show the person abilities that are the maximum likelihood estimates at the current stage of estimation. To make these two sets of estimates coincide, please tighten the convergence criteria in your Winsteps control file: LCONV=.0.001 ; or tighter
If STBIAS=YES is used, then score table measures are dependent on the data array, even if items are anchored. |
-6.34E |
"E" (Extreme, Extrapolated) is a warning that the accompanying value is not estimated in the usual way, but is an approximation based on arbitrary decisions. For extreme scores, the Rasch estimated would be infinite. So the arbitrary decision has been made to make the extreme score more central by the EXTREMESCORE= amount (or its default value), and to report the measure corresponding to that score. The Rasch standard error of an extreme score is also infinite, so the reported standard error of an "E" value is the standard error of the finite reported measure. |
S.E. |
The model-based standard error of the MEASURE, not adjusted for misfit. |
CURRENT VALUES, UMEAN=.0000 USCALE=1.0000 |
This shows the current user-scaling. Changing the user-scaling in the Specification menu dialog box or the Help menu USCALE= calculator changes Table 20 immediately. Use this to experiment with different values of USCALE= and UIMEAN=. |
TO SET MEASURE RANGE AS 0-100, UMEAN=46.5329 USCALE=7.3389 |
Suggested UIMEAN= and USCALE= values for transformation of the MEASUREs into user-friendly values in the range 0-100 resembling percentages. |
TO SET MEASURE RANGE TO MATCH RAW SCORE RANGE, UMEAN=49.2956 USCALE=5.7243 |
Suggested UIMEAN= and USCALE= values for transformation of the MEASUREs into user-friendly values into the range or raw scores so that the MEASUREs resemble raw scores. |
Predicting Score from Measure: Score = Measure * 8.2680 + 38.9511 |
A linear approximation of the score-to-measure ogive useful for predicting raw scores on this set of items from measures. To approximate measures by raw scores: USCALE= 8.2680 and UIMEAN= 38.9511 <- use numbers from your Table 20.1 |
Predicting Measure from Score: Measure = Score * .1158 + -4.5099 |
A linear approximation of the score-to-measure ogive useful for predicting measures from raw scores on this set of items. |
Maximum statistically different levels of performance (strata) = 3.8 Wright's Sample-independent Person (Test) Reliability based on maximum strata = 0.94 |
Across the raw-score range in Table 20.1, statistically significant different raw scores are 1.96 * (M1 - M2) / √(SE12 + SE22) apart where M1 and M2 are the two measures. SE1 and SE2 are their two standard errors. See www.rasch.org/rmt/rmt144k.htm. The number of different levels (strata) resembles a separation index. Wright's matching "Test" Reliability is shown. These are equivalent to the Separation and Reliability of a person sample with a uniform distribution having the range of the MEASUREs in Table 20. |
1
PERSON 1 1123 55247311 6 35411272 12
T S M S T
%TILE 0 10 20 40 50 60 70 80 90 99
ITEM 1 141221 1
T S M S T
%TILE 0 10 60 90 99
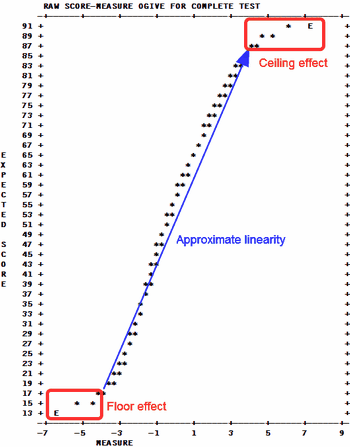
A graph of the score to measure conversion is also reported. '*' indicates the conversion. This is the Test Chracteristic Curve, TCC. Table 20.1 gives the score-to-measure conversion for a complete test, when going from the y-axis (score) to the x-axis (measure). When going from the x-axis (measure) to the y-axis(score), it predicts what score on the complete test is expected to be observed for any particular measure on the x-axis. For CAT tests and the like, no one takes the complete test, so going from the y-axis to the x-axis does not apply. But going from the x-axis to the y-axis predicts what the raw score on the complete bank would have been, i.e., the expected total score, if the whole bank had been administered.
Measure distributions for the persons and items are shown below the score-to-measure table. M is the mean, S is one P.SD (population standard deviation) from the mean. T is two P.SDs from the mean. %ILE is the percentile, the percentage below the measure. Percentiles have the range 0-99.
Test Information
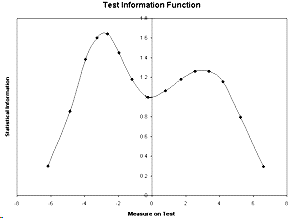
The statistical information is (USCALE/S.E.)². These are plotted in the test information function in the Graph window. You can also plot the values reported in TCCFILE=
Score-to-measure Table 20 is to be produced from known item and rating scale structure difficulties
In your Winsteps control file:
IAFILE=if.txt ; usually values from IFILE=if.txt of another analysis ; the item anchor file containing the known item difficulties
SAFILE=sf.txt ; usually values from SFILE=sf.txt of another analysis ; the structure/step anchor file (only for polytomies)
CONVERGE=L ; only logit change is used for convergence
LCONV=0.0001 ; logit change too small to appear on any report.
STBIAS=NO ; no estimation bias correction with anchor values
TFILE=*
20 ; the score table
*
The data file comprises two dummy data records, so that every item has a non extreme score, e.g.,
For dichotomies:
CODES = 01
Record 1: 10101010101
Record 2: 01010101010
For a rating scale from 1 to 5:
CODES = 12345
Record 1: 15151515151
Record 2: 51515151515
